Local Volatility (LV): What it is, How it Works

What Is Local Volatility (LV)?

Local volatility (LV) is a measure used in quantitative analysis to provide a comprehensive view of volatility. It factors in strike prices and time to expiration from the Black-Scholes model to produce pricing and risk statistics for options. Local volatility is related to implied volatility (IV) and can be extrapolated from it.

While the Black-Scholes model generalizes the volatility level across all options on the same underlying, local volatility allows each individual option to have its own volatility level. This more accurately reflects an option’s true theoretical value.

Key Takeaways

• Local volatility assigns implied volatility to each option based on its strike and expiration.
• This provides a more specific and accurate picture of the volatility surface compared to the Black-Scholes model’s constant volatility.
• Skew and term structure of volatility are employed with local volatility considerations.

Understanding Local Volatility

Local volatility was introduced by economists Emanuel Derman and Iraj Kani. It attempts to identify the actual volatility of an option across various strike prices and expirations. Local volatility uses two-factor analysis to provide a more accurate reading than implied volatility. When plotted, local volatility generally fits the data more closely. Some academics argue that local volatility is the more appropriate input from a logical standpoint, although implied volatility can be used to obtain the correct price.

Instead of relying on a constant volatility function calculated from strike price and expiration, local volatility looks at the asset price and time to answer the question of risk in a different way. This results in a different view of the volatility around an option given the same inputs.

Local volatility is often extrapolated from implied volatility and is sensitive to changes in implied volatility. Small changes in implied volatility can result in drastic shifts in local volatility.

How Local Volatility Is Used

One criticism of the original Black-Scholes model is that it assumes a constant volatility level for the entire life of the option. However, the market produces volatility smile, which became apparent after the 1987 stock market crash. To represent volatility better, academics and traders sought alternatives, and local volatility emerged as one of the products.

Local volatility is particularly useful in pricing exotic options that are difficult to fit into standard models. It can be used to value all combinations of strike prices and expirations compared to implied volatility’s single expiration.

Both local volatility and implied volatility are often studied together and compared to historical volatility. While local and implied volatility are generated from current option price levels using the Black-Scholes model, historical volatility utilizes past data of actual pricing fluctuations.

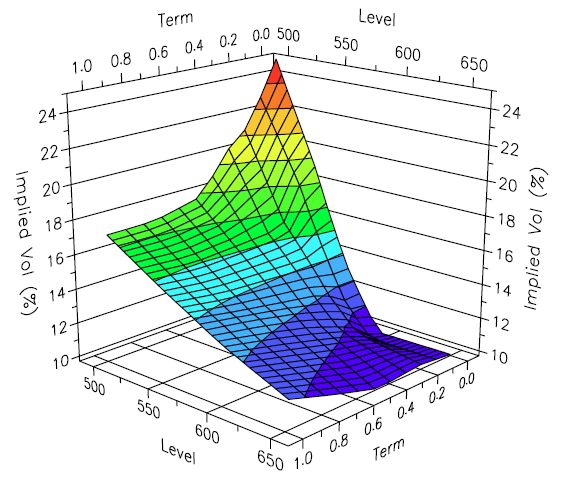
The Volatility Surface

The volatility surface is a three-dimensional plot of local volatilities. The x-axis represents time to maturity, the z-axis is the strike price, and the y-axis is implied volatility. The implied volatility surface should ideally be flat across strike prices and time to maturity if the Black-Scholes model were correct. However, in practice, this is not the case.

The volatility surface is far from flat and often varies over time due to the assumptions of the Black-Scholes model. Options with lower strike prices tend to have higher implied volatilities compared to those with higher strike prices.

As the time to expiration approaches infinity, volatilities across strike prices tend to converge to a constant level.

The term structure of volatility describes how local volatility changes among options with different times to expiration. The volatility surface is often observed to have an inverted volatility smile, where options with a shorter time to maturity have higher volatility compared to options with longer maturities. This observation is more pronounced in periods of high market stress. It should be noted that every option chain is different, and the shape of the volatility surface can be wavy across strike price and time. Additionally, put and call options usually have different volatility surfaces.