Understanding Capital Market Line CML and How to Calculate It
Understanding Capital Market Line (CML) and How to Calculate It
What Is the Capital Market Line (CML)?
The capital market line (CML) represents portfolios that optimally combine risk and return. It is a theoretical concept that represents all the portfolios that optimally combine the risk-free rate of return and the market portfolio of risky assets. Under the capital asset pricing model (CAPM), investors will choose a position on the CML, in equilibrium, by borrowing or lending at the risk-free rate, maximizing return for a given level of risk.
Key Takeaways
– The CML represents portfolios that optimally combine risk and return.
– The CML is a special case of the capital allocation line (CAL) where the risk portfolio is the market portfolio. Thus, the slope of the CML is the Sharpe ratio of the market portfolio.
– The intercept point of the CML and efficient frontier would result in the most efficient portfolio called the tangency portfolio.
– Buy assets if the Sharpe ratio is above the CML and sell if the Sharpe ratio is below the CML.
Formula and Calculation of the CML
Calculating the CML is done as follows:
Rp = rf + (RT – rf)σT/σp
Where:
– Rp = portfolio return
– rf = risk-free rate
– RT = market return
– σT = standard deviation of market returns
– σp = standard deviation of portfolio returns
What the CML Can Tell You
Portfolios that fall on the CML optimize the risk/return relationship, thereby maximizing performance. The capital allocation line (CAL) represents the allotment of risk-free assets and risky portfolios for an investor.
The CML is a special case of the CAL where the risk portfolio is the market portfolio. As a generalization, buy assets if the Sharpe ratio is above the CML and sell if the Sharpe ratio is below the CML.
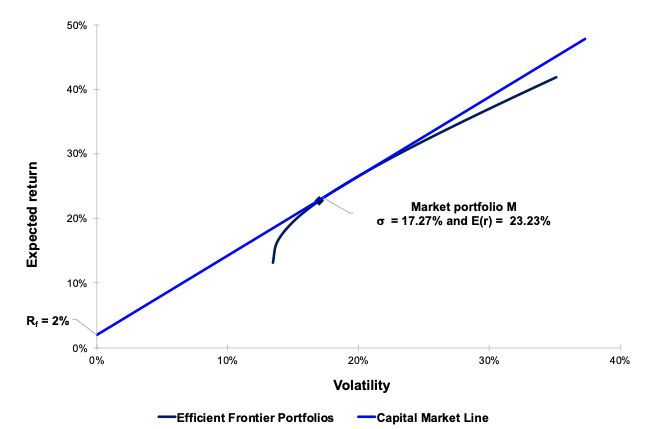
CML differs from the efficient frontier as it includes risk-free investments. The intercept point of the CML and efficient frontier would result in the most efficient portfolio, called the tangency portfolio.
Mean-variance analysis was pioneered by Harry Markowitz and James Tobin. Markowitz identified the efficient frontier of optimal portfolios in 1952, and Tobin included the risk-free rate to modern portfolio theory in 1958. Sharpe developed the CAPM in the 1960s and won a Nobel prize for his work in 1990, along with Markowitz and Merton Miller.
The CAPM is the line that connects the risk-free rate of return with the tangency point on the efficient frontier of optimal portfolios that offer the highest expected return for a defined level of risk, or the lowest risk for a given level of expected return.
Portfolios with the best trade-off between expected returns and variance (risk) lie on this line. The tangency point is the optimal portfolio of risky assets, known as the market portfolio. Under the assumptions of mean-variance analysis, where investors seek to maximize their expected return for a given amount of variance risk and there is a risk-free rate of return, all investors will select portfolios that lie on the CML.
According to Tobin’s separation theorem, finding the market portfolio and the best combination of that market portfolio and the risk-free asset are separate problems. Individual investors will either hold just the risk-free asset or some combination of the risk-free asset and the market portfolio, depending on their risk-aversion.
As an investor moves up the CML, the overall portfolio risk and returns increase. Risk-averse investors will select portfolios close to the risk-free asset, preferring low variance to higher returns. Less risk-averse investors will prefer portfolios higher up on the CML, with a higher expected return but more variance. By borrowing funds at a risk-free rate, they can invest more than 100% of their funds in the risky market portfolio, increasing both the expected return and the risk beyond that offered by the market portfolio.
Capital Market Line vs. Security Market Line
The CML is sometimes confused with the security market line (SML). The SML is derived from the CML. While the CML shows the rates of return for a specific portfolio, the SML represents the market’s risk and return at a given time and shows the expected returns of individual assets. The measure of risk in the CML is the standard deviation of returns, while the risk measure in the SML is systematic risk or beta.
Securities that plot on the CML and the SML are fairly priced. Securities that plot above the CML or the SML are generating returns that are too high for the given risk and are underpriced. Securities that plot below the CML or the SML are generating returns that are too low for the given risk and are overpriced.
Why Is the CML Important?
Portfolios that fall on the CML optimize the risk/return relationship, thereby maximizing performance. So, the slope of the CML is the Sharpe ratio of the market portfolio. As a generalization, investors should look to buy assets if the Sharpe ratio is above the CML and sell if the Sharpe ratio is below the CML.
How Is Capital Allocation Line (CAL) Related to CML?
The CAL represents the allotment of risk-free assets and risky portfolios for an investor. The CML is a special case of the CAL where the risk portfolio is the market portfolio. As an investor moves up the CML, the overall portfolio risk and returns increase. Risk-averse investors will select portfolios close to the risk-free asset, preferring low variance to higher returns. Less risk-averse investors will prefer portfolios higher up on the CML, with a higher expected return but more variance.
Are CML and Efficient Frontier the Same?
CML differs from the efficient frontier as it includes risk-free investments. The efficient frontier is made up of investment portfolios that offer the highest expected return for a specific level of risk. The intercept point of the CML and efficient frontier would result in the most efficient portfolio, called the tangency portfolio.
Are CML and Security Market Line (SML) the Same?
The CML is sometimes confused with the SML. The SML is derived from the CML. While the CML shows the rates of return for a specific portfolio, the SML represents the market’s risk and return at a given time and shows the expected returns of individual assets. The measure of risk in the CML is the standard deviation of returns, while the risk measure in the SML is systematic risk or beta.


