Type 1 Error Definition False Positives and Examples

Type 1 Error: Definition, False Positives, and Examples

What Is a Type I Error?

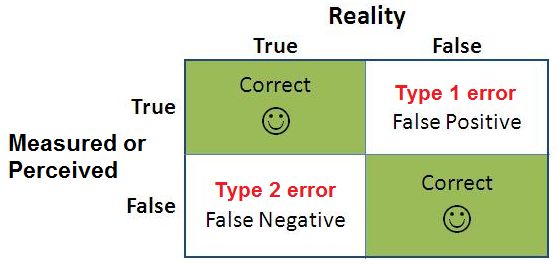
In statistical research, a type 1 error is when the null hypothesis is rejected incorrectly, leading to the study stating that notable differences were found in the variables when there were actually none. Put simply, a type I error is a false positive result.

Making a type I error can’t be avoided because of the uncertainty involved. A null hypothesis is established during hypothesis testing before a test begins. In some cases, a type I error assumes there’s no cause-and-effect relationship between the tested item and the stimuli to trigger an outcome.

Key Takeaways

– A type I error occurs during hypothesis testing when a null hypothesis is rejected, even though it is accurate and should not be rejected.

– Hypothesis testing is a testing process that uses sample data.

– The null hypothesis assumes no cause-and-effect relationship between the tested item and the stimuli applied during the test.

– A type I error is a false positive leading to an incorrect rejection of the null hypothesis.

– A false positive can occur if something other than the stimuli causes the outcome of the test.

How a Type I Error Works

Hypothesis testing is a testing process that uses sample data. The test is designed to provide evidence that the hypothesis or conjecture is supported by the data being tested. A null hypothesis is a belief that there is no statistical significance or effect between the two data sets, variables, or populations being considered. A researcher would generally try to disprove the null hypothesis.

For example, let’s say the null hypothesis states that an investment strategy doesn’t perform any better than a market index like the S&P 500. The researcher would take samples of data and test the historical performance of the investment strategy to determine if the strategy performed at a higher level than the S&P. If the test results show that the strategy performed at a higher rate than the index, the null hypothesis is rejected.

This condition is denoted as n=0. If the result seems to indicate that the stimuli applied to the test subject caused a reaction, the null hypothesis stating that the stimuli do not affect the test subject needs to be rejected.

A null hypothesis should ideally never be rejected if it’s found to be true. It should always be rejected if it’s found to be false. However, errors can occur.

False Positive Type I Error

A type I error is also called a false positive result. This result leads to an incorrect rejection of the null hypothesis, rejecting an idea that shouldn’t have been rejected in the first place.

Rejecting the null hypothesis under the assumption that there is no relationship between the test subject, stimuli, and outcome may sometimes be incorrect. If something other than the stimuli causes the outcome of the test, it can cause a false positive result.

Examples of Type I Errors

Let’s look at a couple of hypothetical examples to show how type I errors occur.

Criminal Trials

Type I errors commonly occur in criminal trials, where juries are required to come up with a verdict of either innocent or guilty. In this case, the null hypothesis is that the person is innocent, while the alternative is guilty. A jury may come up with a type I error if the members find that the person is found guilty and is sent to jail, despite actually being innocent.

Medical Testing

In medical testing, a type I error would cause the appearance that a treatment for a disease reduces the severity of the disease when it does not. When testing a new medicine, the null hypothesis will be that the medicine does not affect the progression of the disease.

Let’s say a lab is researching a new cancer drug. Their null hypothesis might be that the drug does not affect the growth rate of cancer cells.

After applying the drug to the cancer cells, the cancer cells stop growing. This would cause the researchers to reject their null hypothesis that the drug would have no effect. If the drug caused the growth stoppage, rejecting the null hypothesis would be correct.

However, if something else during the test caused the growth stoppage instead of the administered drug, this would be an example of an incorrect rejection of the null hypothesis (a type I error).

How Does a Type I Error Occur?

A type I error occurs when the null hypothesis, which is the belief that there is no statistical significance or effect between the data sets considered in the hypothesis, is mistakenly rejected. The type I error should never be rejected even though it’s accurate. It is also known as a false positive result.

What Is the Difference Between a Type I and Type II Error?

Type I and type II errors occur during statistical hypothesis testing. While the type I error (a false positive) rejects a null hypothesis when it is, in fact, correct, the type II error (a false negative) fails to reject a false null hypothesis. For example, a type I error would convict someone of a crime when they are actually innocent. A type II error would acquit a guilty individual when they are guilty of a crime.

What Is a Null Hypothesis?

A null hypothesis occurs in statistical hypothesis testing. It states that no relationship exists between two data sets or populations. When a null hypothesis is accurate and rejected, the result is a false positive or a type I error. When it is false and fails to be rejected, a false negative occurs. This is also referred to as a type II error.

What’s the Difference Between a Type I Error and a False Positive?

A type I error is often called a false positive. This occurs when the null hypothesis is rejected even though it’s correct. The rejection takes place because of the assumption that there is no relationship between the data sets and the stimuli. As such, the outcome is assumed to be incorrect.

The Bottom Line

Hypothesis testing is a form of testing that uses data sets to either accept or determine a specific outcome using a null hypothesis. We often use hypothesis testing in different areas of life, such as making investment decisions or deciding the fate of a person in a criminal trial. Sometimes, the result may be a type I error, which is the incorrect rejection of the null hypothesis even when it is true.