Type II Error Explained Plus Example vs Type I Error
Type II Error Explained, Example & vs. Type I Error
What Is a Type II Error?
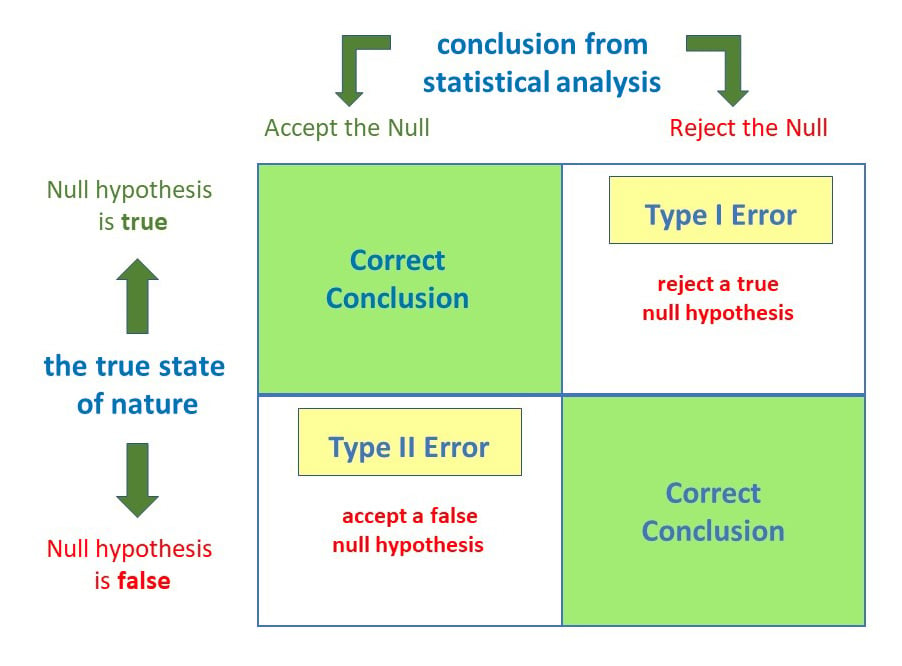
A type II error is a statistical term used in hypothesis testing that describes the error that occurs when one fails to reject a false null hypothesis. It produces a false negative, also known as an error of omission. For example, a test for disease may report a negative result when the patient is infected. This is a type II error because we accept the incorrect conclusion of the test as negative.
A Type II error can be contrasted with a type I error, which is the rejection of a true null hypothesis. The error rejects the alternative hypothesis, even though it does not occur by chance.
Key Takeaways
– A type II error is the probability of incorrectly failing to reject the null hypothesis.
– It is essentially a false negative.
– Making more stringent criteria for rejecting a null hypothesis can reduce type II errors, but it increases the chance of a false positive.
– Risk of error is influenced by sample size, true population size, and the pre-set alpha level.
– Analysts should consider the likelihood and impact of both type II and type I errors.
Understanding a Type II Error
A type II error, also known as an error of the second kind or a beta error, accepts a false finding as true. It fails to reject the null hypothesis, even though the alternative hypothesis is true. To reduce the chances of a type II error, more stringent criteria for rejecting a null hypothesis can be implemented, but this may increase the risk of a type I error.
Type I Errors vs. Type II Errors
A type I error rejects a true null hypothesis, while a type II error does not reject a false null hypothesis. The probability of a type I error is determined by the chosen significance level, while the probability of a type II error is equal to one minus the power of the test.
Example of a Type II Error
Imagine a biotechnology company comparing the effectiveness of two diabetes drugs. The null hypothesis states that the drugs are equally effective, while the alternative hypothesis suggests they are not. The company conducts a clinical trial with 3,000 patients, using a significance level of 0.05.
If the drugs are not equal, the null hypothesis should be rejected. However, if the company fails to reject the null hypothesis, a type II error occurs.
The Difference Between Type I and Type II Errors
A type I error is a false positive, rejecting a true null hypothesis. A type II error is a false negative, failing to reject a false null hypothesis.
What Causes Type II Errors?
Type II errors often occur due to low statistical power. Increasing the statistical power by adjusting sample size can help minimize the risk of a type II error.
Factors Influencing the Magnitude of Risk for Type II Errors
The magnitude of risk for type II errors decreases with a larger sample size and a larger true population effect size. The pre-set alpha level also influences the risk, as a lower alpha level increases the risk of a type II error.
How Can a Type II Error Be Minimized?
It is impossible to fully prevent type II errors, but increasing the sample size can minimize the risk. However, this may increase the risk of a type I error.
The Bottom Line
A type II error in statistics is a false negative or the failure to reject a false null hypothesis. It can occur when there is insufficient power in statistical tests, often due to small sample sizes. Increasing the sample size can help reduce the risk of a type II error. Type II errors are distinct from type I errors, which are false positives.