Log-Normal Distribution Definition Uses and How To Calculate

Log-Normal Distribution: Definition, Uses, and How To Calculate

Definition of Log-Normal Distribution

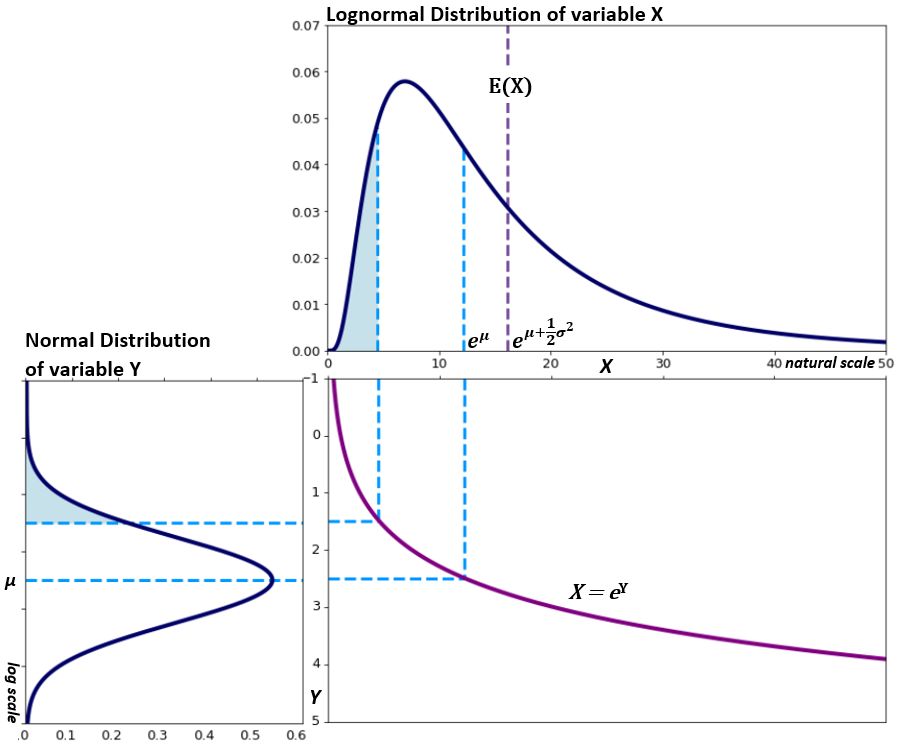
A log-normal distribution is a statistical distribution of logarithmic values from a related normal distribution. It can be translated to a normal distribution and vice versa using logarithmic calculations.

Understanding Normal and Lognormal

A normal distribution is a symmetrical probability distribution that forms a bell curve. 68% of the results fall within one standard deviation, and 95% fall within two standard deviations.

While most people are familiar with a normal distribution, a log-normal distribution may be less known. It can be obtained by converting a normal distribution using logarithmic mathematics. Log-normal distributions can only come from a normally distributed set of random variables.

Log-normal distributions are used in conjunction with normal distributions for several reasons. They are often the result of taking the natural logarithm, with a base of e=2.718. However, the log-normal distribution can be scaled using a different base, which affects its shape.

In general, the log-normal distribution plots the logarithm of random variables from a normal distribution curve. The logarithm is the exponent to which a base number must be raised to produce the random variable (x) found along the normal distribution curve.

Applications and Uses of Log-Normal Distribution in Finance

Log-normal distributions are used to solve problems that normal distributions present. Unlike normal distributions, log-normal distributions only include positive variables and therefore can’t have negative random variables.

One common application of log-normal distributions in finance is the analysis of stock prices. The potential returns of a stock can be graphed using a normal distribution, while the prices of the stock can be graphed using a log-normal distribution. This allows for a better identification of the compound return that the stock can achieve over time.

Note that log-normal distributions have a positively skewed shape with long right tails, which is due to low mean values and high variances in the random variables.

Lognormal Distribution in Excel

Excel provides the LOGNORM.DIST function to calculate lognormal distributions. It is defined as follows:

"Returns the lognormal distribution of x, where ln(x) is normally distributed with parameters mean and standard_dev."

To calculate LOGNORM.DIST in Excel, you will need the following inputs:

– x: value at which to evaluate the function

– Mean: the mean of ln(x)

– Standard Deviation: the positive standard deviation of ln(x)

(Note: The phrase "Standard Deviation = the standard deviation of ln(x) which must be positive" appears twice and can be removed.)