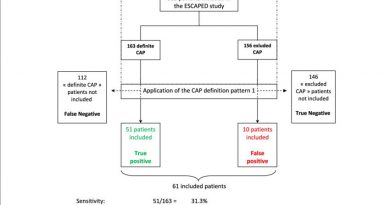
Uniform Distribution Definition How It Works and Example

Uniform Distribution: Definition, How It Works, and Example

What Is Uniform Distribution?

In statistics, uniform distribution refers to a type of probability distribution where all outcomes are equally likely. A deck of cards has a uniform distribution because the probability of drawing any suit is equally likely. Similarly, a coin toss has a uniform distribution because the probability of getting heads or tails is the same.

Key Takeaways

– Uniform distributions have equally likely outcomes.

– In a discrete uniform distribution, outcomes have the same probability.

– In a continuous uniform distribution, outcomes are continuous and infinite.

– Normal distributions have data around the mean occurring more frequently.

– Data occurrence decreases as you move farther from the mean in a normal distribution.

Understanding Uniform Distribution

There are two types of uniform distributions: discrete and continuous. Rolling a die provides an example of a discrete uniform distribution. You can roll a number from 1 to 6, but not a decimal or fraction. Therefore, the roll of a die generates a discrete distribution with an equal probability for each outcome.

Some uniform distributions are continuous. An idealized random number generator would have a continuous uniform distribution where every point between 0.0 and 1.0 has an equal chance of appearing.

There are other important continuous distributions such as the normal distribution, chi-square, and Student’s t-distribution.

Visualizing Uniform Distributions

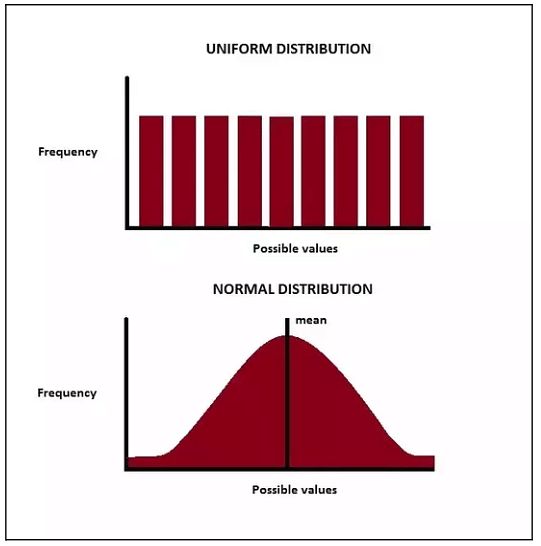
A distribution is a way to visualize data, showing which values have higher or lower chances of occurring. Under a uniform distribution, each value has the same possibility. This distribution can be represented as a rectangle, with each potential outcome having the same height.

For example, when rolling a single die, each number has a 16.67% chance of occurring. The distribution is represented by a horizontal line on a graph.

Uniform Distribution vs. Normal Distribution

Probability distributions help determine the probability of future events. One commonly used distribution is the normal distribution, which shows how continuous data is distributed. In a normal distribution, most data is concentrated around the mean. The area under the curve equals 1, and the frequency of data decreases as it moves away from the mean.

Discrete uniform distributions show that variables in a range have the same probability of occurring. The shape of this distribution resembles a rectangle, with an area under the graph equal to 1.

Example of Uniform Distribution

In a traditional deck of cards, there are 52 cards with four suits. Removing the jokers and face cards leaves 40 cards, a discrete data set.

For example, the probability of pulling a 2 of hearts from this deck is 2.5%. Each card is unique, so the probability of pulling any card is the same.

The likelihood of pulling a heart is significantly higher, as there are only four suits. The probability of pulling a heart is 25%.

Uniform Distribution FAQs

What Does Uniform Distribution Mean?

Uniform distribution is a probability distribution where the outcomes of a discrete set of data have the same probability.

What Is the Formula for Uniform Distribution?

The formula for a discrete uniform distribution is P(x) = 1/n, where P(x) is the probability of a discrete value and n is the number of values in the range.

Is a Uniform Distribution Normal?

No, a uniform distribution is not normal. Normal distributions show that the probability of a variable occurring around the mean is higher, while a uniform distribution has constant probability.

What Is the Expectation of a Uniform Distribution?

The expectation of a uniform distribution is that all possible outcomes have the same probability.