Trinomial Option Pricing Model What it is How it Works
Trinomial Option Pricing Model: What it is, How it Works
What is Trinomial Option Pricing Model?
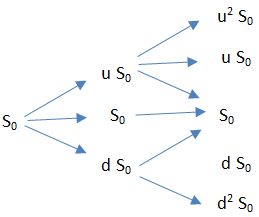
The trinomial pricing model incorporates three possible values for an underlying asset in one time period. These values can be greater than, the same as, or less than the current value.
The model uses an iterative procedure and allows for the specification of nodes or points in time between the valuation date and the option’s expiration date.
Key Takeaways
– The trinomial option pricing model values options using an iterative approach.
– Each iteration can have three outcomes: a move up, a move down, or no change.
– The model is more frequently used in practice compared to the Black-Scholes or binomial models.
Understanding Trinomial Option Pricing Model
Among the many models for pricing options, the Black-Scholes and binomial models are the most popular.
The Black-Scholes model, also known as the Black-Scholes-Merton model, determines the price of a European call option and other financial instruments. The binomial model uses an iterative procedure and nodes to determine the option’s price.
The trinomial model is useful for pricing American options and embedded options. It is simple to model but limited by the three possible values the underlying asset can have in one time period. This is not realistic as assets can have any number of values within a range.
The trinomial option pricing model, proposed by Phelim Boyle in 1986, is considered more accurate and efficient than the binomial model.
Trinomial vs. Binomial Models
The trinomial model differs from the binomial option pricing model by incorporating another possible value in one time period. In the binomial model, it is assumed that the value of the underlying asset will either be greater or less than its current value.
However, the trinomial model incorporates a third possible value, where there is no change in value over a given time period. This assumption aligns more closely with real-life situations, where the value of an asset may remain constant for a certain period.
For exotic options that are more complex than commonly traded vanilla options, the trinomial model may be more stable and accurate.